에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스가 발견한 소수 구하기 알고리즘이다.
알고리즘
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. (위는 120까지가 예시)
- 짝수 중 유일하게 2는 소수이므로 2는 소수로 체크해준다. (빨간색)
- 2를 제외한 2의 배수를 모두 지워준다.
- 3은 소수이므로 3은 소수로 체크해준다.(초록색)
- 3을 제외한 3의 배수를 모두 지워준다.
- 5는 소수이므로 5는 소수로 체크해준다.(파란색)
- 5를 제외한 5의 배수를 모두 지워준다.
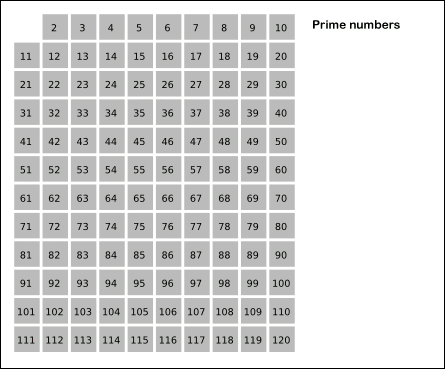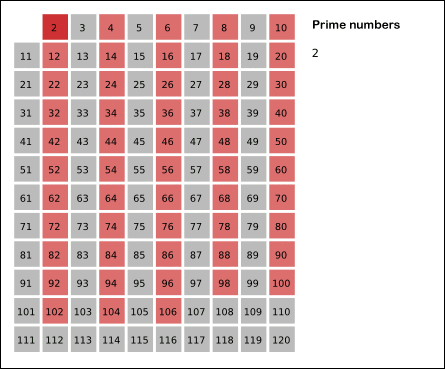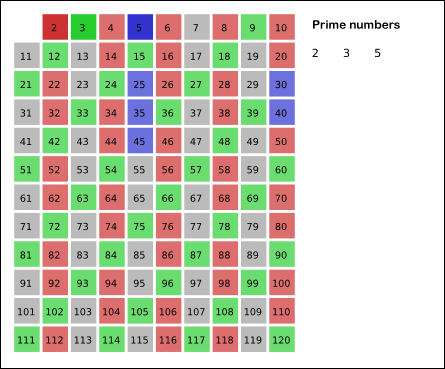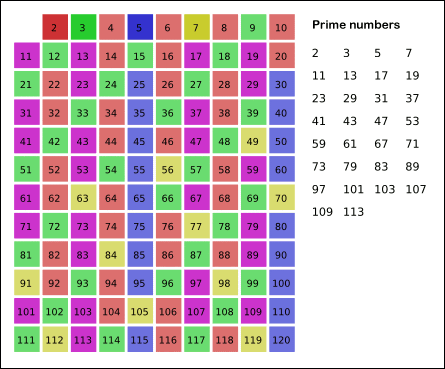
- ... 3~4단계의 과정을 소수를 만날때마다 해주면된다.
간단하게 말해서, 본인이 설정한 범위의 최댓값을 x라고 한다면,
2부터 시작해서 x까지 소수의 배수를 다 지워버리면 된다.
코드(C++)로는 아래와 같이 나타낼 수 있다.
void Eratos(int n)
{
/* 만일 n이 1보다 작거나 같으면 함수 종료 */
if (n <= 1) return;
/* 2부터 n까지 n-1개를 저장할 수 있는 배열 할당
배열 참조 번호와 소수와 일치하도록 배열의 크기는
n+1 길이만큼 할당(인덱스 번호 0과 1은 사용하지 않음) */
bool* PrimeArray = new bool[n + 1];
/* 배열초기화: 처음엔 모두 소수로 보고 true값을 줌 */
for (int i = 2; i <= n; i++)
PrimeArray[i] = true;
/* 에라토스테네스의 체에 맞게 소수를 구함
만일, PrimeArray[i]가 true이면 i 이후의 i 배수는 약수로 i를
가지고 있는 것이 되므로 i 이후의 i 배수에 대해 false값을 준다.
PrimeArray[i]가 false이면 i는 이미 소수가 아니므로 i의 배수 역시
소수가 아니게 된다. 그러므로 검사할 필요도 없다.
또한 i*k (k < i) 까지는 이미 검사되었으므로 j시작 값은 i*2에서 i*i로 개선할 수 있다.
*/
for (int i = 2; i * i <= n; i++)
{
if (PrimeArray[i])
for (int j = i * i; j <= n; j += i)
PrimeArray[j] = false;
}
// 이후의 작업 ...
}
주석중에 i*k 까지는 이미 검사되었으므로 j시작 값은 i*2에서 i*i로 개선할 수 있다. 라는 부분이있다.
이 문장을 예시를 들어 설명하자면,
예를들어 i가 5가 되기 이전까지 이미 반복문을 완료했다면, 앞의 2,3,4에서 2*5, 3*5, 4*5까지 모두 완료했을 것이다.
따라서 5*5부터 즉, i*i부터 하면 된다는 말이다.
그리고 배열 초기화 부분에서 모두 true로 초기화 하게 되는데,
반복문으로 모두 초기화하는 방법도 있지만,
fill_n(PrimeArray, n+1, true);fill_n(초기화할 배열 이름, 범위, 초기화 할 값)으로 초기화가 가능하다.
