이 알고리즘은 플로이드 알고리즘, 로이-워셜 알고리즘, 로이-플로이드 알고리즘, 또는 WFI 알고리즘으로 알려져 있다.
알고리즘
Floyd-Warshall 알고리즘은 그래프에서 지날 수 있는 모든 경로를 비교한다.
시간 복잡도는 O(n^3)으로, 코드로 짜면 3중의 중첩 반복문을 가진다.
노드i에서 노드j까지 가는 방법은 2가지 중 하나일 것이다. (중간에 k란 노드가 있다고 하자)
- i에서 바로 j로 가는 경우
- i에서 k를 거쳐 j로 가는 경우
위 2가지의 경우의 수 중에서 최단경로가 결국 우리가 구하고자 하는 값이 된다.
따라서 아래와 같이 나타낼 수 있다.
floyd(i,j,k) = min(i에서 j로 가는 최단거리, i에서 k로 가는 최단거리 + k에서 j로 가는 최단거리)
코드로 나타내면 아래와같다. (C++)
for(int k = 1; k<= n; k++){
for(int i = 1; i <= n; i++){
for(int j = 1; j<=n; j++){
dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]);
}
}
}
예시
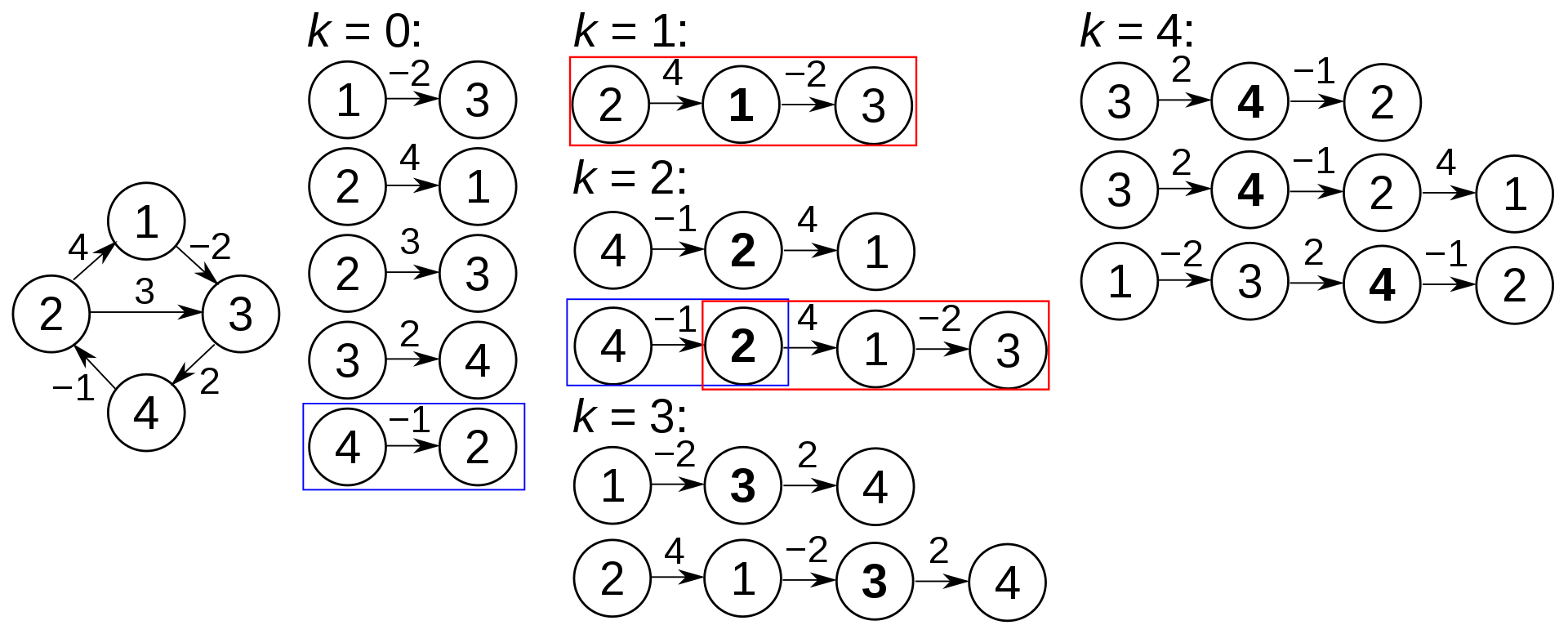
맨 왼쪽의 예시 그래프로 위 코드를 적용하여 k의 변화에 따라 흐름을 나타낸 그림이다.
k는 중간에 지나쳐야 하는 노드이다.
따라서 k가 0일때는 중간에 아무것도 없이 한칸만 이동하는 것이라고 생각하면 된다.
파란박스는 k=0일때의 최단거리이고, 빨간박스는 k=1일때의 최단거리이다.
k=2일때 4에서 3으로 가는 루트를 보면 위의 두 값을 이용한 것을 볼 수 있다.
위의 예시를 알고리즘 설명에서 나타낸 것 처럼 해보자.
floyd(4,3,2)가 된다.
4에서 3까지 중간에 2가있을때 최단거리를 구하는 것이다.
만약 4->3의 간선이 있었다면,
floyd(4,3,2) = min(4에서 3으로 가는 거리, 4에서 2로 가는 거리 + 2에서 3으로 가는 거리)가 된다.
min의 2번째 인자는 위 그림에서 보면 결국 파란박스 + 빨간박스가 되는것이다.
