문제
19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.
택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
D(T1,T2) = |x1-x2| + |y1-y2|
두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.
따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합
반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을
작성하시오.
입력
첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를,
둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
예제 입력 1
1
예제 출력 1
3.141593
#include <iostream>
using namespace std;
const double PI = 3.14159265358979323846;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
double r;
cin >> r;
double euclid, taxi;
euclid = PI * r * r;
taxi = r * r * 2;
cout << fixed;
cout.precision(6);
cout << euclid << '\n' << taxi << '\n';
return 0;
}유클리드 기하학의 방법은 우리가 흔히 원의 넓이를 구할 때 사용하는 방법이다.
그런데 택시 기하학이 처음 봤을때는 좀 이해가 안갈수도 있다. (나도...)
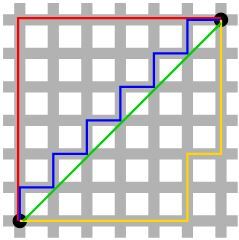
위의 그림에서 점 사이의 거리를 나타낼 때, 초록색 선이 유클리드 기하학 방법이고, 빨간선이 택시 기하학 방법이다.
기하학에서 원은 한점에서 같은 거리에 있는 점의 집합으로 표현된다. 그런데, 택시 기하학에서는 거리의 정의가 다르다 보니 원의 모습도 다르게 나타난다.
예를 들어 정수 격자 좌표계에서 한 점에서 거리가 2인 점들의 집합을 나타내면 이와 같다. 그리고, 격자의 크기를 계속해서 줄여 나가서 격자의 크기가 0 인 극한(실수좌표계)을 생각해 보면 원의 모습은 이렇게 된다. 즉, 흔히 말하는 마름모꼴 형태의 정사각형이 된다.

유클리드 기하학의 원의 방정식은 (x-a)^{2}+(y-b)^{2}=r^{2} 이지만,
택시 기하학에서의 원의 방정식은 원의 중심이 (a,b) 이고, 거리가 d 일때 아래와 같이 표현된다.
|x - a| + |y - b| = d
따라서 마름모의 넓이를 구하는 공식은, 두 대각선끼리의 곱 / 2 이기 때문에,
대각선의 길이는 반지름 * 2 이므로 2r * 2r / 2 = 2r^2이 된다.
'PS > 백준' 카테고리의 다른 글
| 백준 / 브루트포스 / 2798번 / 블랙잭 / C++ (0) | 2022.01.17 |
|---|---|
| 백준 / 수학 / 1002번 / 터렛 / C++ (0) | 2022.01.15 |
| 백준 / 수학 / 3009번 / 네 번째 점 / C++ (0) | 2022.01.14 |
| 백준 / 수학 / 9020번 / 골드바흐의 추측 / C++ (0) | 2022.01.14 |
